RAMANUJAN- GREATEST LOGICAL MIND OF INDIA!!!
Ramanujan was born in Erode, a small village in Tamil Nadu on 22 December 1887. When he was a year old his family moved to the town of Kumbakonam, where his father worked as a clerk in a cloth merchant’s shop. When he was nearly five years old, Ramanujan enrolled in the primary school. In 1898 he joined the Town High School in Kumbakonam. At the Town High School, Ramanujan did well in all subjects and proved himself an able all round scholar. It was here that he came across the book Synopsis of Elementary
Results in Pure Mathematics by G. S. Carr. Influenced by the book, he began working on mathematics on his own, summing geometric and arithmetic series.
He was given a scholarship to the Government College in Kumbakonam. However his scholarship was not renewed because Ramanujan neglected all subjects other than mathematics. In 1905 he appeared for the
First Arts examination which would have allowed him to be admitted to the University of Madras. Again he failed in all subjects other than mathematics, a performance he repeated in 1906 and 1907 too. In the following years he worked on mathematics, with only Carr’s book as a guide, noting his results
in what would become the famous Notebooks.
He got married in 1909 and started looking for a job. His search took him to many influential people, among them Ramachandra Rao, one of the founding members of the Indian Mathematical Society. For a year he was supported by Ramachandra Rao who gave him Rs. 25 per month. He started posing and solving problems in the Journal of the Indian Mathematical Society. His research paper on Bernoulli numbers, in 1911, brought him recognition and he became well known in Chennai as a mathematical genius. In 1912,
with Ramachandra Rao’s help, he secured the post of clerk in the accounts section of the Madras Port Trust.
He continued to pursue mathematics and in 1913 he wrote to G. H. Hardy in Cambridge, enclosing a long list of his own theorems. Hardy immediately recognized Ramanujan’s mathematical ability. On the basis of Hardy’s letters, Ramanujan was given a scholarship by the University of Madras in 1913. In 1914, Hardy arranged for him to go to Trinity College, Cambridge.
Ramanujan’s work with Hardy produced important results right from the beginning. In 1916 Ramanujan graduated from Cambridge with a Bachelor of Science by Research. In 1918, he was elected a Fellow of the Cambridge Philosophical Society, a Fellow of the Royal Society of London, and a Fellow of Trinity College, Cambridge, all in the same year! However, from 1917 onwards he was seriously ill and mostly bedridden. In 1919 he returned to India, in very poor health.
Other mathematicians' views of Ramanujan
Ramanujan is generally hailed as an all-time great like Leonhard Euler, Carl Friedrich Gauss, and Carl Gustav Jacob Jacobi, for his natural mathematical genius. G. H. Hardy quotes: "The limitations of his knowledge were as startling as its profundity. Here was a man who could work out modular equations and theorems... to orders unheard of, whose mastery of continued fractions was... beyond that of any mathematician in the world, who had found for himself the functional equation of the zeta function and the dominant terms of many of the most famous problems in the analytic theory of numbers; and yet he had never heard of a doubly-periodic function or of Cauchy's theorem, and had indeed but the vaguest idea of what a function of a complex variable was...".
Quoting K. Srinivasa Rao, "As for his place in the world of Mathematics, we quote Bruce C. Berndt: 'Paul Erdős has passed on to us G. H. Hardy's personal ratings of mathematicians. Suppose that we rate mathematicians on the basis of pure talent on a scale from 0 to 100, Hardy gave himself a score of 25, J.E. Littlewood 30, David Hilbert 80 and Ramanujan 100.'"
In his book Scientific Edge, noted physicist Jayant Narlikar stated that "Srinivasa Ramanujan, discovered by the Cambridge mathematician G.H. Hardy, whose great mathematical findings were beginning to be appreciated from 1915 to 1919. His achievements were to be fully understood much later, well after his untimely death in 1920. For example, his work on the highly composite numbers (numbers with a large number of factors) started a whole new line of investigations in the theory of such numbers."
A common anecdote about Ramanujan relates to the number 1729. Hardy arrived at Ramanujan's residence in a cab numbered 1729. Hardy did not think highly of Ramanujan's interest in recreational mathematics, and so claimed this number to be uninteresting. Ramanujan is said to have stated on the spot that it was actually a very interesting number mathematically, being the smallest number representable in two different ways as a sum of two cubes:
Generalizations of this idea have spawned the notion of "taxicab numbers".
Coincidentally, 1729 is also product of 3 prime numbers
by
Indi Proff
http://indiproff.blogspot.com/
Courtesy: tifr, wiki



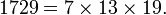
No comments:
Post a Comment